Home >> Waves, resonance

Damping

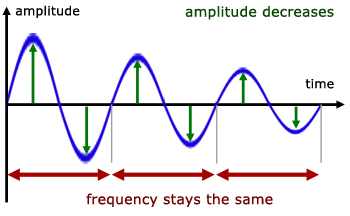
Damping describes the loss of energy of an oscillatory motion. The loss of energy is evident in the reduction in amplitude of the wave. Successive waves become smaller, however, the frequency remains the same.
One common example is the pendulum. After being set in motion, the distance being swept out by the pendulum bob becomes progressively smaller. Energy is lost to the system due to air resistance and friction at the support.

back to top

Forced vibrations

Forced vibration can be illustrated by a simple experimental setup called Barton's pendulums.

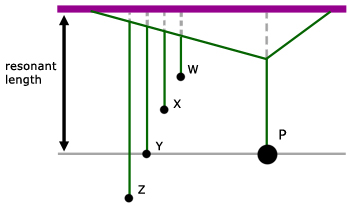
Essentially a large pendulum is used to provide a driver frequency which will make the other, smaller pendulums oscillate at the same rate. This driver frequency is in fact the natural frequency of the pendulum. The frequency at which it would oscillate at without the smaller pendulums. The masses of the smaller pendulums are insignificant compared to the mass of the larger. So their effect is not of any consequence.

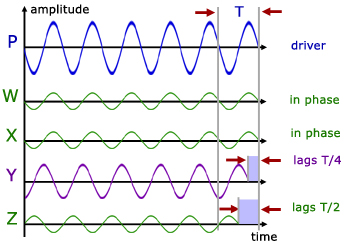
On the graph it should be noted:

1. All the pendulums have the same frequency.

2. Pendulum Y has the same length as P but is not in phase with it. It is approx. 1/4 period behind. However, Y does oscillate with greater amplitude than the other small pendulums. Y is said to be resonating with P.

3. The shorter pendulums, W & X are approx. in phase with P.

4. Pendulum Z is approx. 1/2 period behind P.

Using Barton's pendulums to investigate forced vibrations

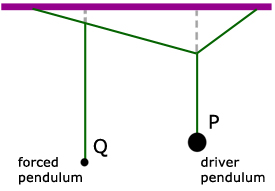
The method is to keep the length of the dependent pendulum Q the same, while varying the length of the driver pendulum P.

Measurements are then made of:

1) the frequency of P

2) the frequency of Q

3) the amplitude of Q

4) the phase difference between P and Q

Initial graphs(blue) are draw for the amplitude of Q and the phase difference of Q against driver frequency.

Various levels of damping are then applied to Q. Families of curves are produced.

More damping is produced by decreasing the bob mass of Q and/or adding cardboard fins to increase air resistance.

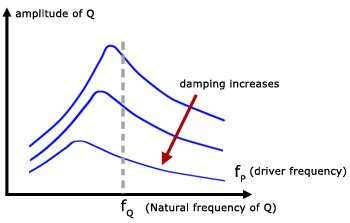
It can be seen that the amplitude of pendulum Q is maximum (maximum resonance) just before the natural frequency of the driver pendulum P.
If Q is heavily damped the amplitude is much less at its maximum and occurs at a much lower frequency than the natural driver frequency.

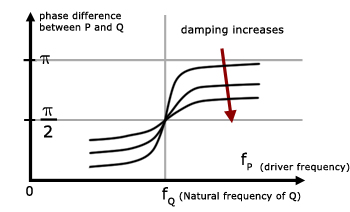
Whether pendulum Q has light or heavy damping, it always has a phase difference of π/2 radians (90^o) with P, at the natural frequency with which P oscillates.

For higher driver frequencies and light damping the phase difference rises to a maximum of π (pi) radians (180^o).

Higher driver frequencies and heavy damping produce a phase difference only slightly above π/2 radians.

back to top

implications & uses of resonance

implications:

1. Soldiers must 'break step' when crossing wooden bridges.

2. Cars/aircraft/rockets are carefully designed so that parts do not resonate producing unwanted noises/dangerous vibrations.

3. Electrical audio circuits are subject to 'feedback' . This is the loud howling sound produced when a microphone is too close to a loudspeaker and the amplifier gain is too high.

uses:

1. clocks & watches - quartz crystals resonate producing accurate timing frequencies

2. standing waves in pipes

3. ultra-sonic cleaning - dirt particles resonate with the applied frequency and are dislodged

4. crystal radios - circuits resonate at the same frequency as a radio station

5. radio antennas (aerials) - resonate when they interact with radio waves

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]