Home >> Matter, elasticity

Young's Modulus

This is a typical stress-strain curve of a ductile material. A brittle material would have a much smaller strain value before breaking(making EB shorter).

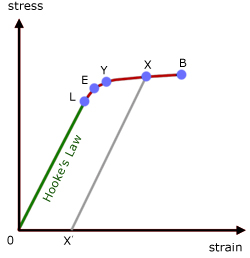
L - limit of proportionality
E - elastic limit
Y - yield point
X - stress removed here, body has permanent      strain 0X^'
B - breaking stress

For a given material, by definition, Young's Modulus (E) is the ratio of stress* to strain*, provided the limit of proportionality is not exceeded.
* sometimes referred to as stress σ (sigma), strain ε (epsilon)

The gradient at any point on a stress - strain graph is the Young's Modulus (E).

back to top

Hooke's Law and molecular separation

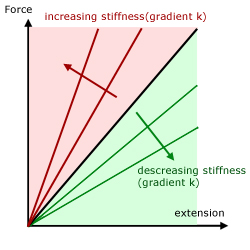
Hooke's Law states that the extension(x) of a spiral spring(or other elongated body) is proportional to the applied force(F), provided the limit of proportionality is not exceeded.

k is the constant of proportionality(a measure of 'stiffness')

So force-extension curves of different materials are straight lines through the origin, with gradient k.

On a stress-strain graph the Young's Modulus is constant for the portion of the graph where Hooke's Law applies. This can be easily shown by substituting for k=F/x into the equation for E.

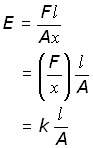
E is a constant because l, A and k are all constant.

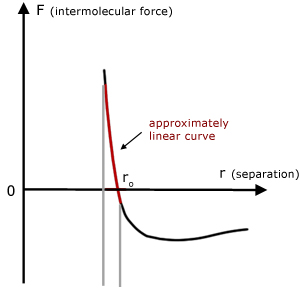
The force F between molecules is directly proportional to small displacements either side of the equilibrium position r_o . This translates in the bigger picture to applied force being proportional to extension.

back to top

Strain Energy

To obtain an expression for the strain energy(work done) in stretching a wire, consider a wire of original length l₀ where a force F produces an extension x . It is assumed that the wire obeys Hooke's Law.

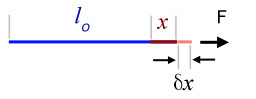
Now, let the force F cause a further extension δx, , where δx is so small that F may be onsidered constant.

Since

work done = force x distance force moves

The total work done when the wire is stretched from 0 to x is the area under the F- x curve between these two limits.

Since the wire obeys Hooke's Law,

Substituting for F in the integral expression(above):

,         

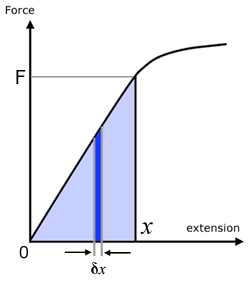
As can be seen from the graph, the area under the curve is half the product of F and x .

back to top

Elastic Hysteresis

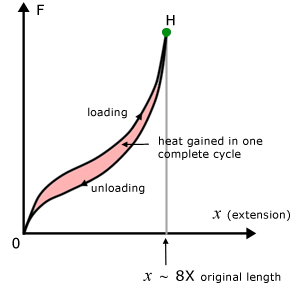
The graph illustrates how for a given force, the extension is greater for unloading than loading.
Looking at this another way, for a given extension the loading force is greater than the unloading force.
The stretching produces an increase in temperature(loading), but when the strain is reduced(unloading) the temperature drops. However, some heat is retained to keep the material above its initial temperature.
For a complete cycle, the increase in heat energy is the area of the hysteresis loop.
The graph is for rubber, but metals also exhibit this property, though the effect is considerably smaller.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]