Home >> Waves, Huygens Construction
intro |
||
Introduction
To understand Huygens' Construction it is important to know the relation between wavefronts and rays.
A wavefront represents the leading edge of one complete wave. So the perpendicular distance between two wavefronts represents one wavelength.
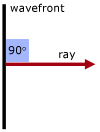
A ray is simply the direction of travel of a wavefront. Hence wavefronts and rays are always at right angles to each other.
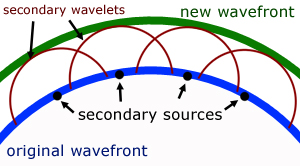
Huygens' postulate
Huygens postulated that points on the wavefronts themselves were the source of small waves and that they combined to produce further wavefronts.
Refraction
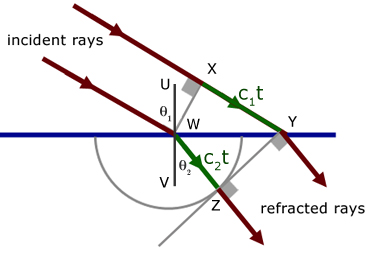
Consider the wavefront WX at right angles to two parallel incident rays.
c1 is the velocity of light in the medium above the blue line
c2 is the velocity of light in the medium below the blue line
Let t be the time interval for the wavefront to travel from X to Y.
When the wavefront WX enters the medium (below the blue line) a wavelet of radius c2t is produced.
The new wavefront is found by drawing a tangent to the circle from Y.
If the tangent meets the circle at point Z, then the new wavefront is YZ.
Using some simple geometry, an important relationship can be found relating the angle of incidence θ1 , the angle of refraction θ2 with the velocity of light c1 and c2 in the respective media.
Looking at the diagram, around point W ,
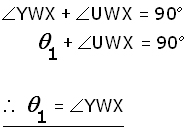
in triangle WYZ ,
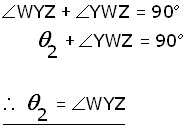
Looking at triangles WXY and WYZ ,
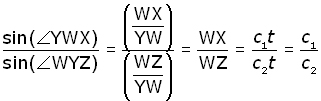
substituting for angles YWX and WYZ from above, this becomes:
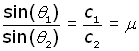
where μ (mu) is the refractive index between the two media.
The effect can be observed in a ripple tank. Water waves travel faster in deeper water than in shallow.
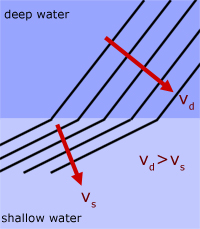
Note the change in wavelength. Wavelength is shortere in shallower water. This is a result of the frequency of the waves being the same, while the wavelength and the velocity can change.
![]()
where,
v is the velocity of the wave
f is the wave frequency
λ is the wavelength
rearranging to make the frequency f the subject,
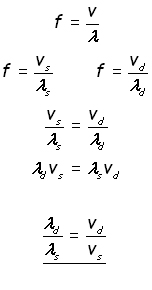
So the ratio of the wavelengths equals the ratio of the velocities.
A high velocity gives a large wavelength.
A small wavelength indicates a low velocity.
Interference - Young's Fringes
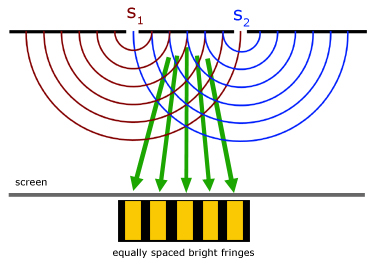
S1 and S2 act as sources of waves in phase with each other.
Bright fringes (yellow) are produced in the directions where light interferes constructively.
On the diagram, this corresponds to where the red and blue lines cross.
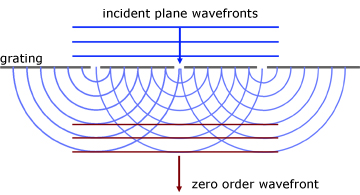
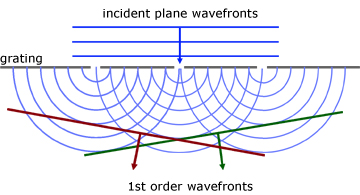
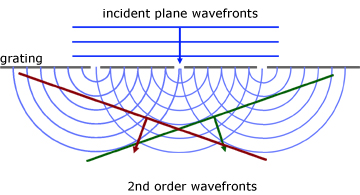
Diffraction Grating
A diffraction grating is a rectangular piece of thin glass with many equally spaced parallel lines ruled on it. A typical grating will have about 600 lines drawn per millimetre.
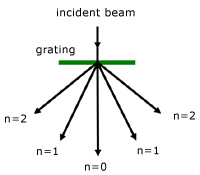
When a parallel beam of monochromatic light is incident normally to a grating, distinct images (maxima) are produced at specific angles.
The effect is described by the equation:
![]()
where
d is the distance between lines
n is the order of the maxima (0, 1, 2 ... )
θ is the angle between the maxima beam and the incident beam
λ is the wavelength of the light
The following sequence of diagrams show how plane wavefronts produce discrete maxima at specific angles.
Water waves at a gap
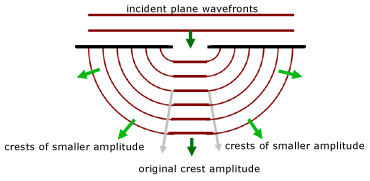
As the gap enlarges, the two edges act as centres for circular waves.
It is observed that the circular waves have smaller crests than the plane waves passing through the middle.
Notice that the lengths of the wavefronts passing through the gap get wider. The grey arrows indicate the change. This demonstrates diffraction at an edge.
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
