Home >> Mechanics, 2D motion, projectiles

Vertical & horizontal components of velocity

When a particle is projected under gravity at a velocity u at an angle θ to the horizontal (neglecting air resistance) it follows the curve of a parabola.

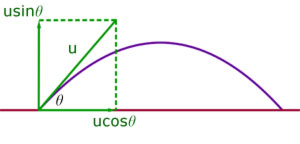
The particle has an initial horizontal speed of ucosθ, which is unchanged throughout the motion.

Vertically the particle has an initial speed of usinθ. It falls under gravity and is accelerated downwards with an acceleration of g ms^-1,where g = 9.8 ms^-2 (approx.)

back to top

Time of flight

The time of flight is calculated from the vertical component of the velocity. It is the time it takes for the particle to go up, reach its maximum height and come down again. So this is twice the time to maximum height.

If the time to maximum height is t secs. Then the time of flight is 2t.

Consider motion up to maximum height. This is attained when the final velocity v = 0.

back to top

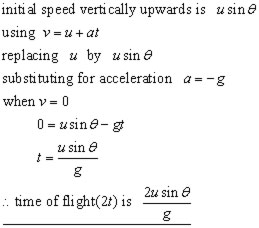
Maximum height attained (H)

The maximum height attained occurs when the particle is momentarily stationary, before falling under gravity. The vertical component of speed is zero at this point(v=0).

back to top

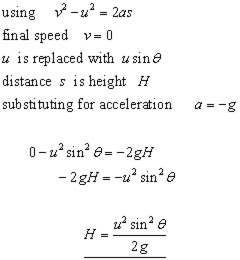
Range(R)

The range is simply the horizontal component of speed multiplied by the time of flight.

back to top

Velocity(speed & direction) at time t

Solution of problems is to find the vertical component of speed at time t and combine this with the original horizontal component of speed, which remains unchanged.

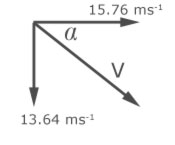
Example

A particle P is projected at an angle of 45 degrees to the horizontal at a speed of 30 ms^-1 .
What is the speed and direction of the particle after 3 secs.?
(g=9.8 ms^-2)

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]