Home >> Fields, electrostatic fields 1

Law of Electrostatics

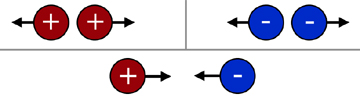
Like charges repel, while unlike charges attract.

The convention for charge relates to early electrostatic experiments with particular materials.

glass rubbed with silk gives a positive charge

ebonite rubbed with fur gives a negative charge

Using these results materials and particles are assigned charge:

perspex(positive), polythene(negative),

electrons(negative), protons(positive) etc.

The decision to make the charge from glass and silk positive, and the charge from ebonite and fur negative was completely arbitrary. The two charges could easily have been transposed, resulting in a positive charge on the electron!

back to top

Coulomb's Law

The force F between two point charges Q₁ & Q₂ is directly proportional to the product of the charges and inversely proportional to the square of the distance r between them.

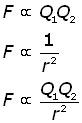
Making the proportionality into an equation by introducing a constant k :

The value of k is given by :

Hence the Coulomb's Law equation becomes :

The quantity ε is called the permittivity. It has a value depending on the medium surrounding the charges.

The symbol ε_o (epsilon nought) is used to describe the permittivity of free space, ie a vacuum.

The value of ε_o can be found from 'Maxwell's equations'. The result includes another constant μ_o (mu nought).

μ_o is called the magnetic permeability of free space.

The two are connected by the following relation, where c is the velocity of light :

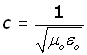
The unit of charge is the coulomb (C). This is a S.I. derived unit.
By definition, a coulomb is the charge passed when a current of 1 ampere flows for 1 second.

1 C = 1 AS^-1

back to top

Electric field strength E

The electric field strength at a point is equal to the force on a unit charge at the point.

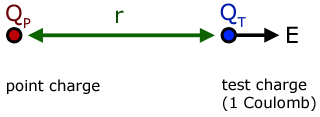
From Coulomb's Law,

where,

Q_T is a unit test charge (1 C )

Q_P is any charge at a point

By definition, electric field strength is force/unit charge. So at the point where charge Q_T is positioned the field strength E is given by :

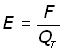
But Q_T is a unit charge, therefore E = F .

Substituting for F in the initial Coulomb's Law equation,

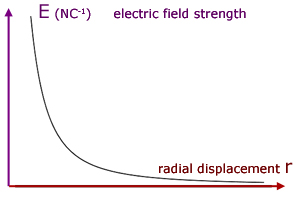
We can now see how electric field strength E varies with distance r from the point.

back to top

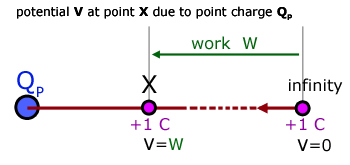
Electric potential V

The electrical potential V at a point in an electric field is defined as:

being numerically equal to the work done W in transferring a unit positive charge from infinity to the point.

From Coulomb's law, the force between two point charges Q₁ and Q₂ is given by :

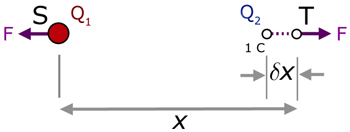
Q₁ is positive at point S. Q₂ is also positive but at point T.

Q₁ exerts a repulsive force F on Q₂.

Q₂ exerts a repulsive force F on Q₁ .

Consider an external force moving Q₂ at T an infinitesimal distance δx towards Q₁ at S.

Because the distance δx is so small, the repulsive force F may be considered to be constant during the movement.

Using,

work = force x distance force moves

the work done δW is given by :

The negative sign indicates that work is done against the field. That is, the motion is in the opposite direction to the direction of repulsion.

Substituting into this equation for F, from the Coulomb's Law equation (above) :

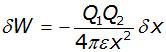
Therefore the total work W done in bringing the charge Q₂ from infinity to a point a distance r from S (where x = r) is given by:

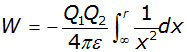
integrating between the limits of r and infinity,

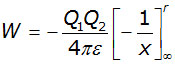
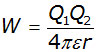
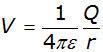
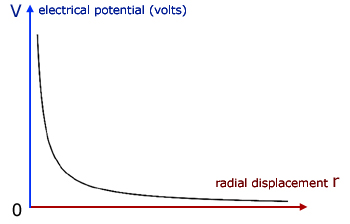
The curve follows a simple inverse relation similar to y = 1/x .

back to top

Electric potential difference

The potential difference between two points in an electric field is numerically equal to the work done in moving a unit + charge from the lower potential point to the higher.

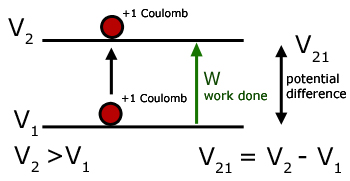
From the definition of potential comes the definition of the volt, with specific units for work and charge.

The potential difference between two points is 1 volt if one joule of energy is used in moving 1 Coulomb of charge between the points.

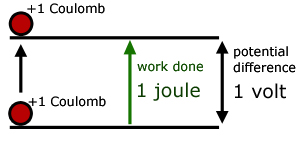
Simply put, the number of volts is equal to the energy involved in moving 1 Coulomb of charge between points. So a 12V battery produces 12J of energy for every Coulomb moved between its terminals.

The equation connecting work W, charge Q and potential difference V is as follows :

(joules = Coulombs x volts)

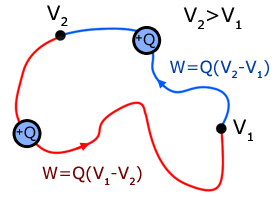
The diagram below illustrates that the work done in taking charge around a closed loop is zero.

Work W is done by the electric field in moving the charge from V₁ to V₂ .

However, work -W must be done against the field to return the charge back to V₁ .

So the sum amount of work done = W + (-W) = 0

back to top

Relation between E and V

Consider a charge +Q being moved by a force F from an arbitrary point A to another point B against an electric field of strength E.

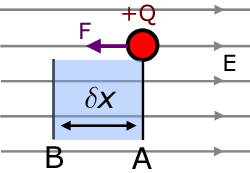
The distance moved, δx , is very small, such that the force F may be considered constant.

Hence the work done δW by the force is :

The force is equal to the force exerted by the field on the charge, but in the opposite direction(note negative sign).

Substituting in the original equation for F gives :

From the definition of potential difference, W = QV .

Therefore, if the potential difference between A & B is δV :
( V_B > V_A )

Substituting for δW ,

cancelling the Q's and rearranging,

In the limit as δV and δx tend to zero,

Multipling both sides by -1 :

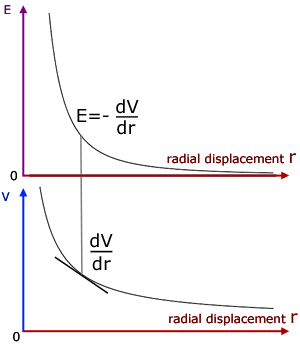
The E-r and V-r graphs below show the relation clearly.
The gradient of the V-r graph is negative. So the negative of its gradient gives a positive value for E in the E-r graph.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]