Home >> Thermal, kinetic theory

Main assumptions of the Kinetic Theory

1. all the molecules of a particular gas are equal

2. collisions between molecules and their container are completely elastic

3. collisions between molecules themselves are completely elastic

4. the size of actual molecules is negligible compared to molecular separation

5. the laws of Newtonian mechanics apply

6. extremely large numbers of molecules mean that statistical methods can be applied

7. between collisions molecules move in straight lines at constant speed

8. the motion of molecules is random

9. gravitational effects are negible

10. the time for each collision is negligible

back to top

Derivation of equations

The first step in understanding this theory is to appreciate the momentum change when a particle rebounds from a collision with a wall.

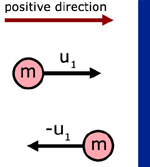
initial mtm. in the x-direction        = mu₁

final mtm. in the x-dir.                  = m( - u₁) = - mu₁

momentum change in the x-dir.   = mu₁ - ( - mu₁) = 2mu₁

Consider a volume of gas in a cuboidal shape of side L.

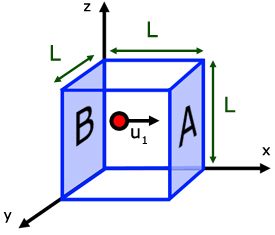
We have seen how the change in momentum of a molecule of gas when it rebounds from one face , is 2mu₁ .

The distance the molecules travels between collisions is 2L.

It collides with face A. Moves a distance L to collide with opposite face B, before returning to face A .

Since speed = distance/time,           time = distance /speed

Therefore the time (t) it takes for the molecule to traverse this distance 2L is given by:

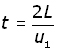
The rate of momentum change (dp/dt) in this time interval is given by:

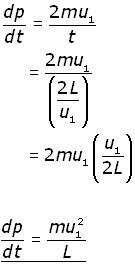
From Newton's 2nd Law, applied force is equal to the rate of change of momentum.

The molecule therefore exerts a force F on the wall, given by:

Since pressure (p) = force/area , the pressure on wall A produced by a single molecule is,

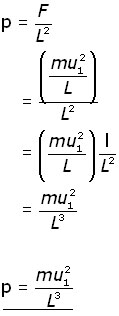
Now, consider all the molecules (N) in the cube and each of their x-component velocities (u₁ u₂ u₃ . . . u_N).

The pressure on wall A becomes:

where,

is the mean square velocity of molecules in the x-direction

The density ( ρ rho ) of the gas is given by:

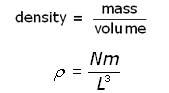
Substituting for into the equation for pressure p

Up to now we have considered the velocity of a molecule in one direction. Now, let us consider the resultant velocity of a molecule in three dimensions.

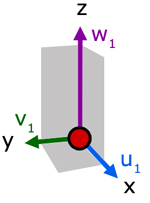
In the diagram, molecule velocity (c₁) is resolved into x, y and z directions. The value of each component is respectively, u₁, v₁ and w₁.
Side d is the projection of c₁ on the x-y plane.

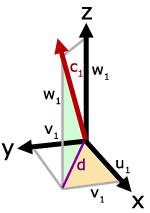
Using Pythagoras' Theorem,

substituting for d² in the second equation,

The equation represents component velocities for one molecule.

Replacing these velocities with mean square velocities, the equation now applies for all molecules.

We make the assumptions that there are very large numbers of molecules and their motion is random. So we can say that mean square velocity components are equal to one another.

So molecular velocity c in terms of components becomes,

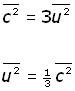
Substituting for into the equation for pressure previously obtained,

back to top

Molecular KE and temperature

Multiplying the Kinetic Theory equation for pressure by V, (the volume of the gas) we obtain:

                 (i            

but density ρ (rho) is given by:

making the mass M the subject, (where M is the mass of gas)

substituting for ρV into the Kinetic Theory equation (i ,

                 (ii            

With some simple arithmetic and a more detailed description of M, this equation can be amended into a more useful form:

If N is the total number of molecules and m is the mass of one molecule:

Now, substituting for 1/3 and M into equation (ii ,

The ideal gas equation is,

where,

n is number moles of gas
R is the Universal Gas Constant
T is the temperature in kelvin

Elimenating pV between the last two equations,

Making the subject of the equation,

                 (iii            

The Avagadro Number N_A is by definition the number of molecules per mole. It is obtained by dividing the total number of molecules by the number of moles of matter:

We can now modify equation (iii to include N_A by substituting for n/N ,

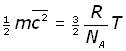
By definition the Boltzmann's constant k is given by:

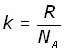
So the final form of the equation is:

is called the average translational KE of a molecule

So the average kinetic energy of gas molecules is proportional to the temperature.

This can also be said in the converse: temperature is a measure of the average kinetic energy of gas molecules

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]