Home >> Fields, gravitational fields 4

[][ ]

[][]

Gravitational potential - U

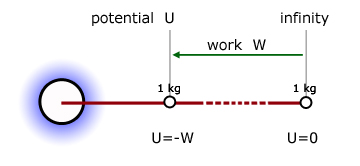
The potential U at a point in a gravitational field is defined as being numerically equal to the work done by the field in bringing a unit mass from infinity to the point.

By definition, the potential at infinity is zero.

where,

U is the gravitational potential at a point

W is the work done in bringing a mass m from infinity to that point.

The units for gravitational potential (work/mass) are Jkg^-1 .

In the treatment of escape velocity(gravitational fields 2) the work done in moving a mass m from the surface of the Earth to infinity was given by:

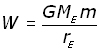
Now if we make the mass unity(m = 1 kg), the energy difference between the 1 kg mass on the surface of the Earth and at infinity (zero potential) is W .

However, since the highest potential is zero at infinity, all potential energies relative to this level are less than zero (ie negative).

Our 1 kg mass on the Earth therefore has a potential of - W .

If U_E is the potential on the surface of the earth, then:

substituting for W from above(remembering that m = 1kg),

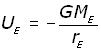
Therefore in the general case, the potential U_r at a point a distance r away from a large mass M is given by:

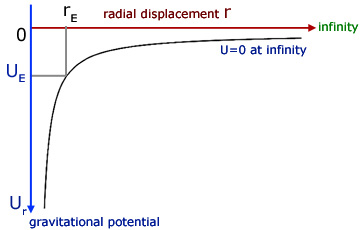
The shape of the curve of U_r against r is of the type y = - x^-1 which is a reflection of the curve y = x^-1 about the x-axis.

back to top

Gravitational field strength - g

The field strength g at a point in a gravitational field is defined as the force on unit mass at the point.

So the unit of gravitational field strength is Nkg^-1 .

From Newton's Law of gravitation, the force on a mass m as a result of a mass M at a distance r is given by:

making the mass m unity (1 kg),

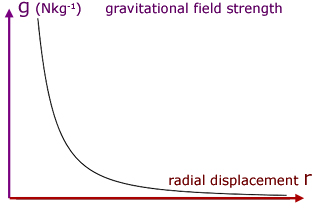
The shape of the curve of g against r is of the type y = x^-2

Near the surface of the Earth, the value of g is considered to be constant at 9.8 Nkg^-1.
The number should look familiar. This is also g , the acceleration due to gravity 9.8 ms^-2 .

The two g's are exactly the same, with the same dimensions.

back to top

Derivation of the relation between g and U

Consider a particle of mass m in a gravitational field.
In the absence of any applied force, the mass would be attracted to the major body producing the field.

Let the mass be held in position by a force F , acting in the opposite direction to the field direction.

Now if the force F moves the mass a very small distance δx against the field, the work done is given by:

(work = force x distance force moves)

assuming that the force F is constant.

When the mass is static, the net force is zero. Forces are balanced. Since forces are vector quantities, the minus sign signifies opposite direction.

Substituting for F into our original equation,

               (i               

By definition, gravitational potential U is given by:

So δU , the increase in U, is given by:

Substituting for δW from equation (i ,

cancelling the mass m gives,

rearranging, to make -g the subject,

In the limit, , therefore

From the graph it can be seen that the gravitational field strength g at a radius r is equal to minus the value of the gradient of the gravitational potential U .

Note that g is positive because the value of dU/dr itself is negative. Multiplying a negative by a negative gives a positive.

back to top

Energy in orbits

The energy E_r of a satellite of mass m in orbit, of radius r around a large body of mass M, is the sum of the satellite's PE and KE respectively,

This equation can be simplified by elimenating v² .

Recalling the equation describing the circular motion of the satellite,

cancelling r

and making v² the subject.

We can now substitute for v² in the initial energy equation:

So the total energy E_r of the satellite in its orbit is given by:

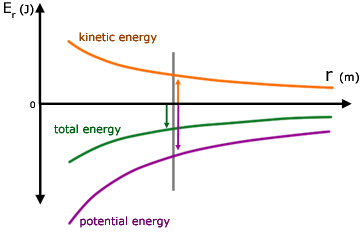
note:

1. the total energy of the satellite is always negative

2. the PE component of the energy is twice as large in absolute terms as the KE component

Also, for any particular circular orbit with radius r , the individual values of kinetic and potential energies are constant.

By contrast, with elliptical orbits the values of potential and kinetic energies are not constant. They vary such that when one is large the other is small and vice versa. It must be remembered that the sum of potential and kinetic energies is always constant for a particular orbit.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]