Home >> Waves, interference of light

Conditions for interference

1. The waves from light sources must be coherent with each other. This means that they must be of the same frequency, with a constant phase difference between them.

2. The amplitude (maximum displacement) of interfering waves must have the same magnitude. Slight variations produce lack of contrast in the interference pattern.

back to top

Young's Double Slit Experiment - Apparatus

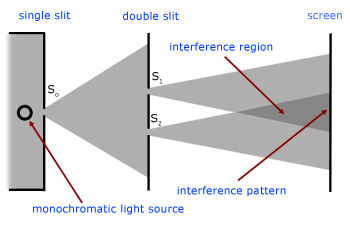
It is important to realise that the diagram is not to scale.

Typically the distance (D) between the double slits and the screen is ~ 0.2 m (20 cm).
The distance (a) between the double slits is ~ 10^-3m (1mm).
The preferred monochromatic light source is a sodium lamp.

back to top

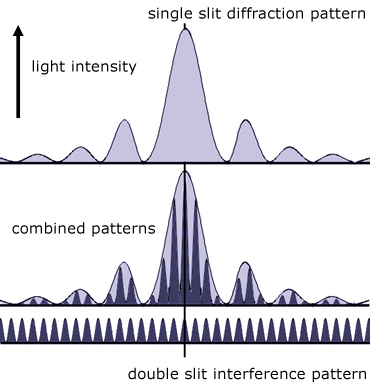
Young's Double Slit Experiment - Display

You will notice some dimming in the image from the centre travelling outwards. This is because the regular light-dark bands are superimposed on the light pattern from the single slit.

The intensity pattern is in effect a combination of both the single-slit diffraction pattern and the double slit interference pattern.

The amplitude of the diffraction pattern modulates the interference pattern.

In other words, the diffraction pattern acts like an envelope containing the interference pattern.

The image above is taken from the central maximum area of a display.

back to top

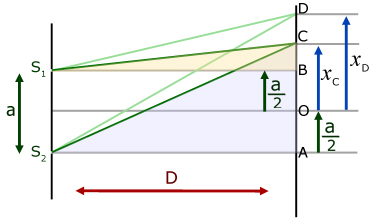
Young's Double Slit Experiment - theory

The separation (y) of bright/dark fringes can be calculated using simple trigonometry and algebra.

Consider two bright fringes at C and D.

For the fringe at C, the method is to find the path difference between the two rays S₁C and S₂C . This is then equated to an exact number of wavelengths n.

A similar expression is found for the fringe at D, but for the number of wavelengths n+1 .

The two expressions are then combined to exclude n .

With reference to triangle CAS₂ , using Pythagoras' Theorem:

substituting for AC and S₂A in terms of x_C , a and D

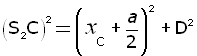            (i

also, with reference to triangle CBS₁

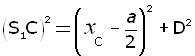            (ii

Subtracting equation (ii from equation (i ,

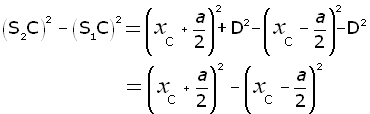
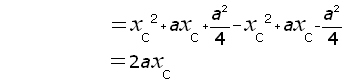
Using 'the difference of two squares' to expand the LHS,

hence,

The path difference S₂C - S₁C is therefore given by:

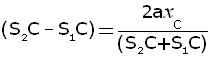
In reality, a ~ 10^-3m and D ~ 0.2 m . The length a is much smaller than D. The two rays S₂C and S₁C are roughly horizontal and each equal to D,

so,

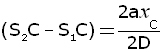
cancelling the 2's,

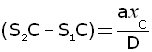
For a bright fringe at point C the path difference S₂C - S₁C must be a whole number (n) of wavelengths (λ).

Hence,

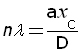
Rearranging to make x_C the subject,

Similarly for the next bright fringe at D, when the path difference is one wavelength longer (n+1),

hence the fringe separation   x_D - x_C is given by,

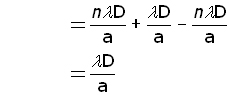
assigning the fringe separation the letter y ,

or with wavelength λ the subject,

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]