Home >> Nuclear, stability: binding energy

Units

To thoroughly understand this work we must have a firm grasp of the units involved:

Joules (J),   electron volts (eV)   and   atomic mass units (u)

There is a discrepancy between the mass of a nucleus and the sum total of the individual masses of its constituents.

This difference is called the mass defect.

We know that energy is equivalent to mass in Einstein's equation,

E = mc²

where E is energy(J), m is mass(kg) and c is the velocity of light (ms^-1).

So the mass can be given in terms of energy. That is in Joules(J).

There is however another energy unit much used in nuclear physics called the 'electron volt' (eV).

One electron volt is the kinetic energy an electron gains when accelerated through a potential difference of 1 volt.

Since,

energy = charge x potential difference

E = eV

e is the charge on the electron 1.602 x 10^-19 Coulomb
V is the p.d., 1 volt in this case

So the energy of 1eV is 1.602 x 10^-19 Joules.

However, there is still another mass unit to consider. This is called the atomic mass unit (u).

By definition 1 u is equal to 1/12 the mass of a carbon-12 atom.

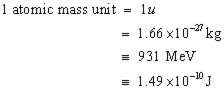
To summarize, mass defects can be given in:

kilograms (kg),   atomic mass units (u),   Joules (J),   electron volts (eV)

.

The key to solving problems on binding energy is to know these units and how they inter-relate to one another.

back to top

Stability

A measure of the stability of an atom is its binding energy per nucleon, usually expressed in MeV (millions of electron-volts).

        binding energy/nucleon = total binding energy for the nucleus/mass number

This is an average of the energy needed to remove a nucleon from the nucleus.

In nuclear reactions energy is released or absorbed as a result of differences in the nuclear binding energy of the original materials and the resulting products.

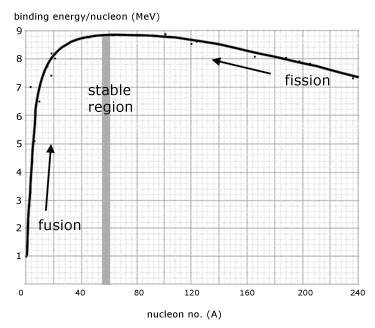
In the graph of binding energy per nucleon against mass number, the following observations can be made as the nucleon number increases:

1. the binding energy/nucleon increases quickly at first then less so, up to a maximum at iron(Fe-56)

2. after iron the binding energy/nucleon slowly decreases

3. less massive nucleons, up to iron, participate in fusion reactions.

4. nucleons more massive than iron participate in fission reactions.

back to top

Reactions

A radioactive reaction procedes because the original nucleus has a greater mass than the mass of its products. Hence there is a mass loss, which manifests itself as energy.

This energy takes the form of the kinetic energy of the products of the reaction or if gamma rays are emitted, their photon energy (E = hv).

Similarly when a nucleus splits into two almost equal parts in a fission reaction. The mass of the original nucleus is greater than the sum of its products.

Fusion reactions obey the same rule. The overall mass of the original nuclei is greater than the mass of the new nucleus and remnants created.

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]