Home >> Waves, Doppler effect
description |
||
Description
The effect is caused by the relative motion of an observer and a source of waves.
The observed frequency(from the observer's viewpoint) is different from the actual frequency. The actual frequency is the frequency emitted from the source.
Derivation of frequency change
To aid understanding, the derivation is best broken down into a number of sections:
observed wavelength - static observer infront of moving source
observed wavelength - static observer behind moving source
observed frequency - moving observer forward of source, moving towards it
observed frequency - moving observer behind source, moving towards it
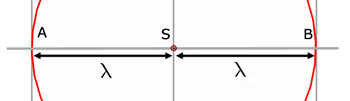
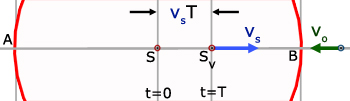
Consider a stationary source of waves S.
A wave is emitted and one period later another wave is just about to be produced.
The separation of successive crests is the wavelength λ .
From the wave equation,
![]()
observed wavelength - static observer infront of moving source
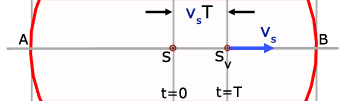
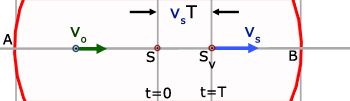
The source moves towards B at velocity vs .
In the time span of one period(T secs.) the source moves towards B a distance vsT (distance = velocity x time) to Sv.
in this time, the first wave has moved from S to B.
The source is considered to carry the second wave. which is on the point of being emitted.
The distance of the crest of the 1st wave at B, measured from S is dW1 .
The distance of the crest of the 2nd wave at Sv , measured from S is dW2 .
![]()
So the distance between crests is given by:
![]() (i
(i
Remembering that,
![]()
we can substitute for T into (i
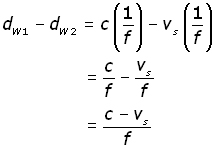
If λF is the wavelength forward of the crests,
(the distance between the crests)
then,
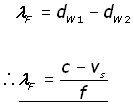
return to 'derivation' sub menu
observed wavelength - static observer behind moving source

This is the same diagram as for the observer infront of the source. But look again, this time from the left at A, looking towards the moving source.
This time we consider the distance between the wave at A and the wave about to be emitted at Sv .
Here the distance moved by the first wave from S and the distance moved by the source are added.
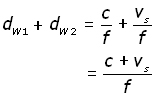
![]()
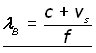
derivation of frequency - moving observer forward of source, moving towards it
vO is the velocity of an observer moving towards the source.
This velocity is independent of the motion of the source.
Hence, the velocity of waves relative to the observer is c + vO .
The wavelength observed forward of the source is therefore given by:
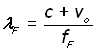
Recalling the equation for 'a static observer infront of a moving source':
![]()
equating these two,
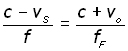
to make fF (frequency forward of the source) the subject
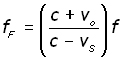
return to 'derivation' sub menu
derivation of frequency - moving observer behind source, moving towards it
Remembering that vO is independent of the motion of the source, the wavelength observed forward of the source is given by:
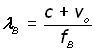
Recalling the equation for 'a static observer behind a moving source':
![]()
equating these two,
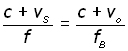
to make fB (frequency behind the source) the subject
return to 'derivation' sub menu
important conclusions:
1. For an observer moving away from the source, the value of vs is negative.
2. The motion of an observer does not alter the wavelength. The increase in frequency is a result of the observer encountering more wavelengths in a given time.
3. When the source is stationary(vs= 0), fA= fB . So it makes no difference whether the observer is infront or behind the source.
Application in astronomy
A star or galaxy having a red shift means that the celestial object is moving away from us. Light rays become more spread out.
A blue shift indicates the opposite. The object is moving towards us. Light rays become bunched up.
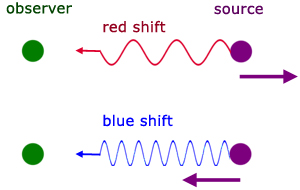
The effects are descriptions of how emission and absorption patterns in spectra are moved either towards the blue or the red end of the spectrum. The movement is apparent when spectra are compared with spectra produced in the lab.
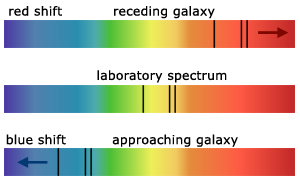
The rotation of celestial objects (eg the Sun, Saturn's rings) can be measured from the light moving towards and away from us at the limb.
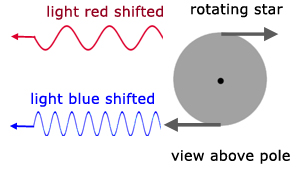
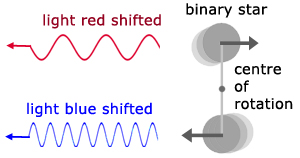
Similarly, double stars are detected by their star-light containing both red shifted and blue shifted lines. This is a result of one star approaching the observer, while the other is receding (a consequence of both stars revolving around a common centre).
Radar speed traps
The speed of an approaching car, or one speeding away, can be found from the change in frequency of microwaves reflected from it.
The following relation is used to calculate vcar the velocity of an approaching/receding car.
![]()
where,
c is the speed of light
f is the frequency of the microwaves
fbeat is the beat frequency produced by interference between the original and reflected waves
Plasma temperature
When the spectrum of a hot plasma is examined, the spectral lines are observed to broaden with increased temperature.
This is because atoms emitting light are moving away from an observer and at the same time coming towards him/her.
Plasmas are extremely hot gases with temperatures in excess of 106 deg. celsius.
The light emitted from an excited atom dropping to a particular energy state would normally be of one discrete wavelength. However, the action of the Doppler effect means that wavelengths of slightly longer and shorter wavelengths are emitted. Hence the spectral line is broadened by the extra wavelengths being produced.
Spectral line broadening is proportional to the square root of the absolute temperature. So by measuring the broadening the temperature can be found.
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
