Home >> Fields, gravitational fields 2

Escape velocity

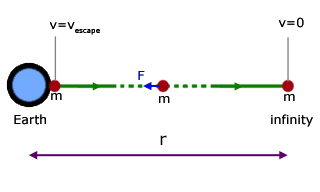
Theoretically (neglecting air resistance) to leave the Earth and not return, a mass must have enough kinetic energy to reach a point an infinite distance away, where its velocity (and hence KE) is zero.

The escape velocity is the minimum initial velocity required to do this. This is a constant for a particular planetary mass, and is independent of the projected mass.

Consider a mass m being projected away from the surface of the Earth with velocity v.

At a distance r from the Earth (mass M_E ) the force of gravity F on the mass is given by:

This equation can be used to calculate the work done by the gravitational force in bringing the mass m to rest.

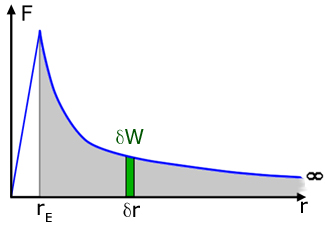
Consider the mass m moving an incremental distance δr (delta r ) away from the Earth. That is, against the force F .

Since work done = force x distance moved against force , the incremental work δW done by the gravitational field on the mass is given by;

substituting for F from the first equation,

Making the expression into an integral, where W is the total work done by the gravitational force between the limits of r = r_E and r = infinity :

(essentially summing the individual slices of F δr between the limits to obtain the area under the curve)

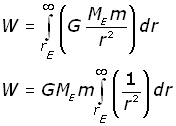
Integrating between the limits,

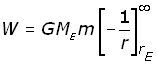
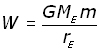
The work done by the gravitational force on the mass equates to the original (maximum) kinetic energy of the mass.

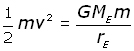
Making the velocity v the subject,

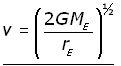
For the Earth, the escape velocity approximates to 11 kms^-1 or 7 miles s^-1.

NB for this theoretical treatment
1. the theory does not apply to continuously propelled masses
2. escape velocity is independent of the direction of projection

back to top

Satellite orbits

A satellite ( mass m) orbits the Earth (mass M_E) at a constant velocity v .

The centripetal force keeping the satellite in orbit is provided by the gravitational force of attraction F between the mass and the Earth.

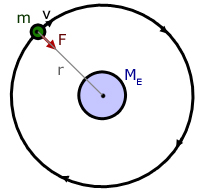
The equations for centripetal and gravitational force are combined.
Satellite velocity v is then made the subject of the equation.

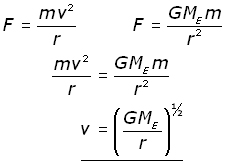
Since G and M_E are constants, satellite velocity is soley dependent on orbital radius.

The period T of the motion is simply the circumference of the circular orbit divided by the satellite's velocity.

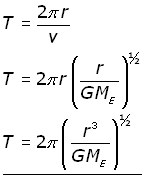
Since G and M_E are constants, orbital period, like orbital velocity, is soley dependent on orbital radius.

back to top

Low orbits

For satellites in orbit a distance equal or less than 200 km above the Earth's surface, the radius of the orbit approximates to the radius of the Earth:

r_E = 6.6 x 10⁶ m       r = 6.8 x 10⁶ m

Making r equal to r_E , the equations for orbital velocity v and period T become:

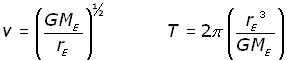
Low Earth orbits are not stable. The outer reaches of the Earth's atmosphere produce drag on a satellite. This changes the satellite's kinetic energy to heat energy, as it is brought back to Earth.

Permanent satellites like the ISS and Hubble have to be given a regular boost to maintain there orbits. Lost kinetic energy is replenished.

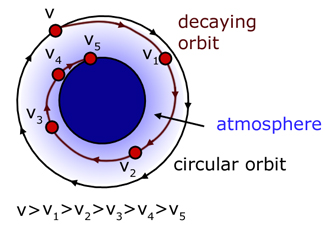
note: The Law of Gravitation predicts that lower orbits have higher velocities. So a satellite should go faster and faster as it moves closer to the Earth. However in this case kinetic energy is lost(as heat energy). The atmosphere brakes the motion. So the law does not apply.

back to top

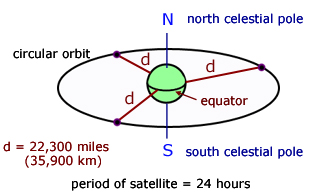
Geostationary orbits

A geostationary satellite is one that always appears in the same place in the sky, no matter what the time of day.

The conditions for this to occur are:

1. the satellite must have an orbital period of exactly 24 hours

2. the satellite must have a circular orbit above the equator

3. the satellite must be orbiting in the same direction as the Earth is rotating

 

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]