Home >> Mechanics, 2D motion, relative motion

One dimensional relative velocity(in a line)

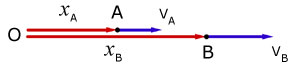
Consider two particles A and B at instant t positioned along the x-axis from point O.

Particle A has a displacement x_A from O, and a velocity V_A along the x-axis.

The displacement x_A is a function of time t .

Particle B has a displacement x_B from O, and a velocity V_B along the x-axis.

The displacement x_B is also a function of time t .

The velocity V_B relative to velocity V_A is written,

_BV_A = V_B - V_A

This can be expressed in terms of the derivative of the displacement with respect to time.

back to top

Two dimensional relative position & velocity

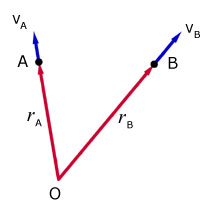
Particle A has a displacement r_A from O, and a velocity V_A along the x-axis.

The displacement r_A is a function of time t .

Particle A has a displacement r_B from O, and a velocity V_B along the x-axis.

The displacement r_B is also a function of time t.

back to top

Relative position

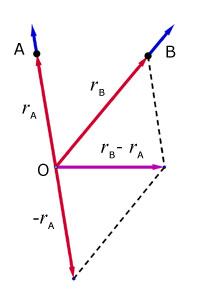
The position of B relative to A at time t is given by the position vector from O, r_B-A .

The position vector r_B-A can be written as,

_Br_A = r_B- r_A

back to top

Relative velocity

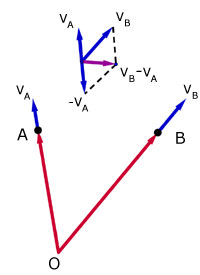
Similarly, at time t the velocity vector V_B relative to velocity vector V_A can be written,

_BV_A = V_B - V_A

This can be expressed in terms of the derivative of the displacement with respect to time.

back to top

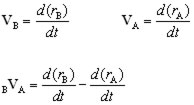
Example #1

If the velocity of a particle P is (9i - 2j) ms^-1 and the velocity of another particle Q is

(3i - 8j) ms^-1 , what is the velocity of particle P relative to Q?

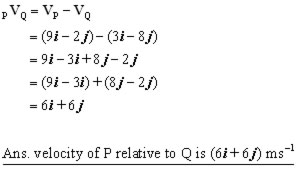
Example #2

A particle P has a velocity (4i + 3j) ms^-1. If a second particle Q has a relative velocity to P of     (2i - 3j), what is the velocity of Q?

back to top

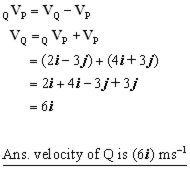
Example #3

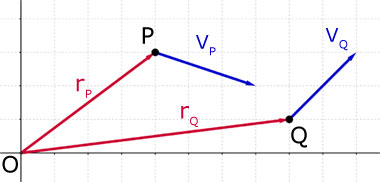
A radar station at O tracks two ships P & Q at 0900hours (t=0) .

P has position vector (4i + 3j) km, with velocity vector (3i - j) km hr ^-1.
Q has position vector (8i + j) km, with velocity vector (2i + 2j) km hr ^-1.

i) What is the displacement of P relative to Q at 0900 hours? (ie distance between ships). Answer to 2 d.p.

ii) Write an expression for the displacement of P relative to Q in terms of time t .

iii) Hence calculate the displacement of P relative to Q at 1500 hours.

iv) At what time are the two ships closest approach and what is the distance between them at this time?

i)

ii)

therefore the displacement of P relative to Q is given by,

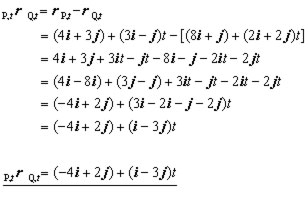
iii) using the result above for 1500 hours( t = 6 )

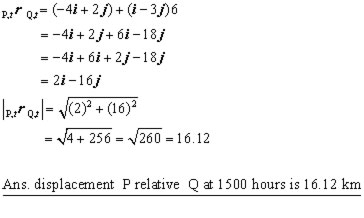
iv) Closest approach is when the position vector of P is at right angles to the reference vector.

The 'reference vector' is the first part of the vector equation for r .

The position vector gives the point P at time t along the straight line described by the vector equation.

(solution to follow)

back to top

Two dimensional relative acceleration

Similarly, if a_A and a_B are the acceleration vectors at A and B at time t,

then the acceleration of B relative to A is given by,

back to top

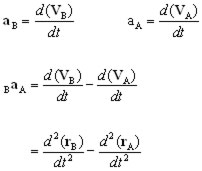
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]