Home >> Quantum, energy levels & ions
energy level diagrams |
||
Visualising energy levels
In an atom, electrons around a central nucleus can only have particular energy values. These discrete values are termed 'energy levels'.
In a diagram they are represented by horizontal lines, with the lowest level (the ground state) at the bottom and the highest level (ionisation) at the top.
The levels are a consequence of the wave nature of electrons, as described by quantum mechanics. Around an atom an electron exists as a particular standing wave, with the number of nodes and antinodes dictated by the quantum number 'n' .
As an example take the simplest atom, the hydrogen atom.
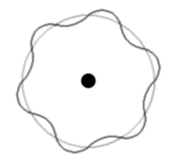
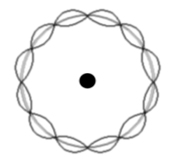
The levels are dictated by concentric wave states of an exact number of electron half wavelengths.
Remember a 'standing wave' (or stationary wave) is the interference between two waves of the same wavelength and speed, travelling in opposite directions.
In the example there are 6 maxima and 6 minima. So the number of half wavelengths is 12.
Therefore the electron state illustrated has n=12.
n |
no. complete waves |
1 |
½ |
2 |
1 |
3 |
1 ½ |
4 |
2 |
5 |
2 ½ |
6 |
3 |
In the energy level diagram(below), energies have to be measured relative to one another. Remember the ground state is the lowest level and ionisation is the highest. So you would expect the ground state be zero. However, that is not the case.
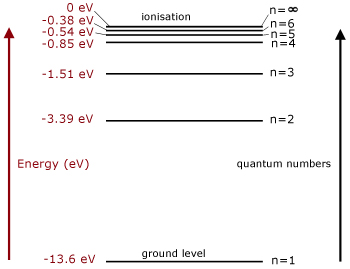
Remember we are measuring potential energy. This is set to zero at infinite distance from the atomic nucleus or molecule. The state is that of an ionised or free electron.
Relative to this state, all the bound electron states have negative potential energy and are measured below it(because they have less energy).
Note that electron energies are expressed in electronvolts.
An electronvolt(eV) is the kinetic energy acquired by an electron, when accelerated through a p.d of 1 volt. Using E=QV the energy is given by e x 1 = 1.6 x 10-19 Joules.
Quantum numbers are given to each energy level. The ground state is n=1, with the n numbers increasing by '1' for each level. The highest energy level, where energy is zero, has n= ∞.
Energy level changes
When radiant energy is absorbed by a bound electron it is excited into a higher energy level. Conversely, when an electron falls to a lower level, radiant energy is given out.
Example: an electron moves down from level 3 to level 1 and gives out a photon of light of frequency ν (nu) .
![]()
substituting for ν from c = νλ and making λ the subject,
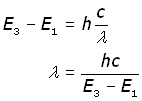
Spectral groups
Looking more closely at the spectrum of hydrogen it is found to be composed of distinct spectral groups.
To understand this we must look in detail at energy level changes. For simplicity we will look at levels from n=4 to levels below.
If an electron is excited up from the ground state (n=1) to level 4, there are four possible paths for it to come back down again to the original state.
| 4 | 4 | 4 | 4 |
| 3 | 3 | ||
| 2 | 2 | ||
| 1 | 1 | 1 | 1 |
If we analyse these transitions/jumps, it is found that they can be divided further into six basic types:
| 4 | 4 | 4 | |||
| 3 | 3 | 3 | |||
| 2 | 2 | 2 | |||
| 1 | 1 | 1 |
The spectrum of hydrogen contains many distinct sets of emission lines. Not all of these are transitions to the ground state or are between intermediary levels.
Three groups of transitions fall between many levels to one particular level in one jump.
These are called:
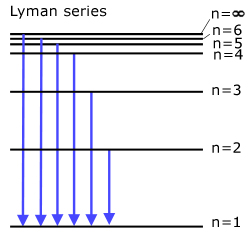
The Lyman series (all transitions directly to ground state )
Light is emitted in the ultra-violet.
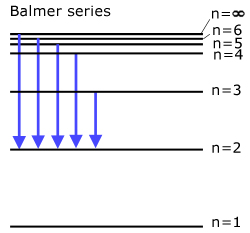
The Balmer series (all transitions directly to state n=2 )
Light is emitted in the visible spectrum.
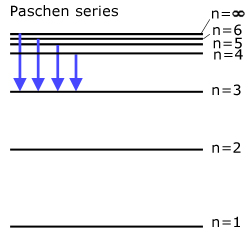
The Paschen series (all transitions directly to state n=3 )
Light is emitted in the infra-red.
Ionisation
In the ground state, where n=1, the electron is not excited and has the least energy.
Remember in energy level diagrams energy is measured upwards. So for electrons reaching higher energy levels it will take less energy to remove them as they are closer to the highest level(ionisation).
The minimum amount of energy to release an electron from the ground state is called the first or principal ionisation energy . The release of electrons in higher states are named as their quantum numbers. For example the second ionisation energy (from level n=2), third ionisation state(from n=3) etc. These principal ionisation energies become smaller and smaller with increasing quantum number, as less energy is required to make up the difference in energy to produce ionisation.
examples:
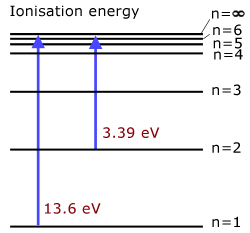
the 1st ionisation energy of hydrogen is 13.6 eV
(level n=1 to ionisation level n=∞ )the 2nd ionisation energy of hydrogen is 3.39 eV
(level n=2 to ionisation level n=∞ )
Excitation Potentials and Energies
Excitation potential is defined as the minimum potential required to excite a free neutral atom from its ground state to a higher state.
Think of a free electron accelerated through a potential and giving up all its energy to an electron in an atom, taking it to a higher energy state. The accelerating p.d. is the excitation potential for that energy change.
examples:
1st excitation potential of hydrogen 10.2 V
(level n=1 to level n=2)2nd excitation potential of hydrogen 12.1 V
(level n=1 to level n=3)
Excitation energy is the energy required to excite an atom from its ground state to a higher state.
examples:
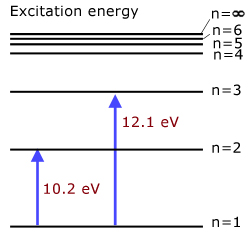
1st excitation energy of hydrogen 10.2 eV
(level n=1 to level n=2)2nd excitation energy of hydrogen 12.1 eV
(level n=1 to level n=3)
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
