Home >> Mechanics, statics, rigid bodies

The Moment of a Force

The moment M (turning effect) of a force about a point O is the product of the magnitude of the force (F) and the perp. distance (x)to the point of application.

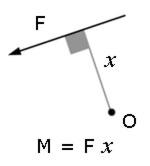
By convention, anti-clockwise moments are positive.

The Principle of Moments

For a rigid body acted upon by a system of coplanar forces, equilibrium is achieved when:

i)  the vector sum of the coplanar forces = 0

ii) there is no net turning effect produced by the forces
(the sum of clockwise & anti-clockwise moments = 0)

Parallel forces acting on a beam

When attempting problems concerning a balance points or fulcrum, remember that there is always an upward force acting.

Example #1   fulcrum near centre

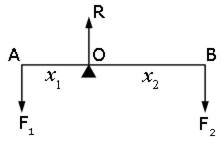
Consider two forces F₁ and F₂ acting vertically downwards at either end of a beam of negligible mass.

When the beam is balanced at its fulcrum O(i.e. horizontal), the sum of the downward forces equals the sum of the upward forces.

If the reaction force at the fulcrum is R,

back to top

Example #2   fulcrum at one end

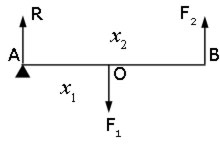
Consider two forces F₁ and F₂ acting on a beam of negligible mass. One force acts vertically downwards near the centre, while the other acts vertically upwards at the end.

When the beam is balanced, the sum of the downward forces equals the sum of the upward forces.

If the reaction force at the fulcrum is R,

back to top

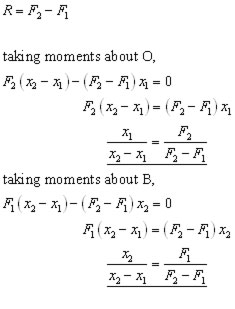
Example #3    a typical problem

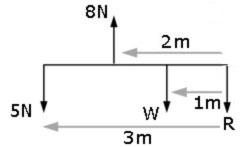
A beam of negligible weight is horizontal in equilibrium, with forces acting upon it, as shown in the diagram.
Calculate the value of the weights R and W.

back to top

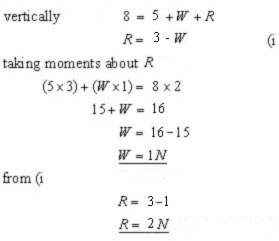
Couples

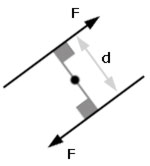
The turning effect of two equal and opposite parallel forces acting about a point equals the product of one force(F) and the perpendicular distance between the forces(d).

couple = F x d

back to top

Centre of Mass

To understand the concept of centre of mass we must first consider a rigid body to be made of an infinite number of particles. Each particle has a gravitational force on it directed towards the centre of the Earth. Assuming these forces are parallel, the weight of the body equals the sum of all the tiny particle weights.

This effective weight may be considered to act through a particular point called the centre of mass(sometimes termed the centroid)

When trying to calculate the centre of mass of a uniform solid eg a cone or hemishpere, we consider the whole mass and its moment about an axis and equate this to the sum of all the moments of constituent masses about the axis. The constituent masses often take the form of thin slices of the regular solid.

Centre of mass of a triangular lamina

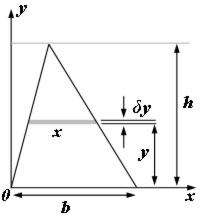
Consider a small horizontal strip of area δA(delta A).

The centre of mass is on a horizontal line a third of the height up from the base

Centre of mass of a hemisphere

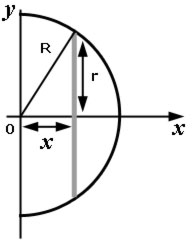
The method of calculation for the centre of mass of a 3D object is very similar to that of a 2D object. In this case we sum thin 2D slices.
The hemispherical axis is the x-axis and this time we consider circular slices of thickness δx.
The radius r of each slice is given by Pythagoras' Theorem:

R² = r² + x²

hence the area of a slice is given by,

Πr² =  Π(R²- x²)

so the volume of a slice δV is given by:

δV = Π(R²- x²)δx

Let the centroid be at position x_C from the origin O.

back to top

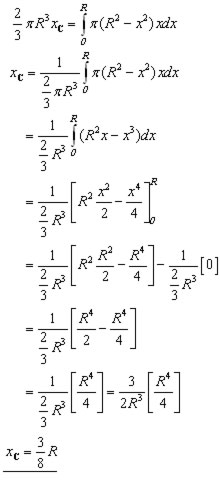
Toppling

  This is to do with a rigid body in contact with a rough plane. Normally the body sits on the plane in equilibrium, with the plane horizontal.
  However if the plane is tilted, this state of affairs only remains until what is called the 'tipping point'. This is when a vertical line passing through the centre of gravity of the body is on the point of falling outside of the body's base area.

When the line falls outside of the base area, the body tips over.

Example

A uniform cuboidal block of dimensions, height 75cm and base 30cm x 50cm rests on a rough plane, with its 50cm side up the plane.
Calculate the angle of inclination of the plane when the block is on the point of toppling(ans. to 1 d.p.)
(assume that the frictional forces on the base of the block are too high for the block to slide)

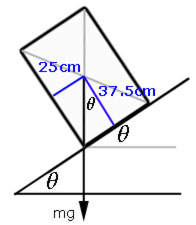
tanΘ = 25/37.5

Θ = 33.7^o

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]