Home >> Waves, waves in strings

The Fundamental Frequency

If we consider a length of string with one end tethered, a wave can be sent from the other end by waving the string up and down. The wave reflects at the tethered end and proceeds in the opposite direction.

Consider now a continuous wave being produced. The wave travelling to the left interferes with the reflected wave moving to the right.
In this way 'standing waves' are set up. The Fundamental Frequency is simply the lowest frequency for a standing wave to form.

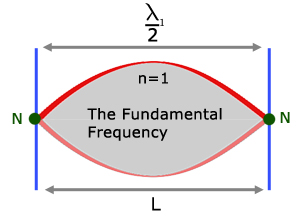
The Fundamental Frequency is just one of a series of particular frequencies called overtones or harmonics, where standing waves form.

back to top

Harmonics and Overtones

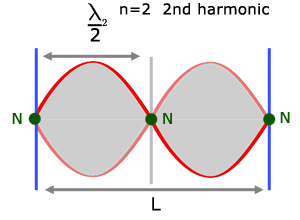
The Fundamental Frequency is called the 1st harmonic. Successive frequencies where standing waves are produced are called the 2nd harmonic, the 3rd harmonic and so on.

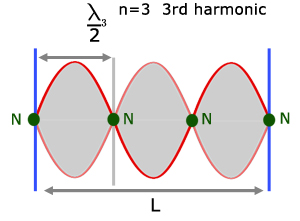
Similarly, the higher frequencies above the Fundamental are termed overtones. The next highest frequency above the Fundamental is called the 1st overtone. The next highest the 2nd overtone etc.

So the 2nd harmonic is the 1st overtone.
The 3rd harmonic is the 2nd overtone etc.

From the diagrams it can be seen that there is a pattern connecting the wavelength(λ) and the length of the string (L).

For the nth harmonic, the wavelength λ_n is given by:

back to top

Frequency theory

First, let us use the familiar wave equation linking velocity, wavelength and frequency,

Hence the frequency of the nth harmonic ( f_n ) is given by:

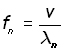                              (i        

where λ_n is the wavelength of the nth harmonic and v is the velocity of the wave in either direction.

From the previous section, the wavelength λ_n is given by:

hence,

substituting for 1/λ_n into equation (i

                             (ii        

With n=1 , frequency of the 1st harmonic (the Fundamental) f₁ is given by:

Substituting for v/2L into equation (ii , we obtain the frequency of the nth harmonic in terms of the Fundamental frequency.

Thus proving that subsequent harmonics are all multiples of the Fundamental Frequency.

back to top

Effect of mass/unit length, length, tension on frequency

By experiment, it can be shown that,

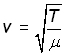                             (iii       

where,
T is the tension in the string - Newtons (N)
μ is the mass/unit length of the string - (kgm^-1)

From equation (ii above,

making v the subject,

substituting for v from equation (iii above,

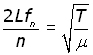
making f_n the subject,

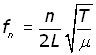
From the equation it can be seen that:

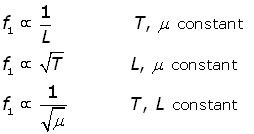
The proportionalities are often termed the Laws of Vibration for Stretched Strings.

In simple terms,

long strings make low frequencies and vice versa;

tight strings make high frequencies and vice versa;

thick, heavy strings make low frequencies and vice versa .

back to top

[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]