Home >> Fields, electrostatic fields 2
field diagrams |
||
Electrostatic field diagrams
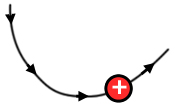
Electric field direction at a point is the direction of a small free moving positive charge if placed at the point.
Point charge electric field patterns:
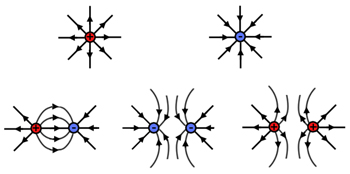
Note the similarity of the patterns with single magnetic poles.
Common solid conductor shapes and their field patterns:
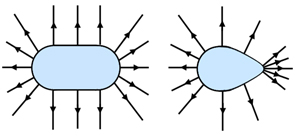
Observe how the field lines are not evenly distributed over each surface. The charge density σ (sigma) is the amount of charge per unit area. As might be expected, the field strength E at a point is directly proportional to σ (Gauss's theorem).
Note how E and σ are higher where the surfaces are highly curved.
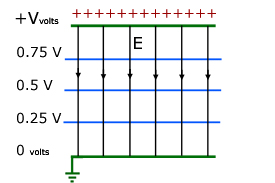
A uniform electric field:
Two oppositely charged and parallel metal plates(X & Y) will produce a uniform electric field E between them. Note, at the edges the field lines are not evenly spaced. So the field there is not uniform.
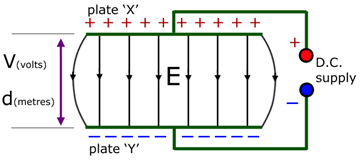
The potential difference between the plates is constant along their length. The potential gradient (the drop in pd with distance) is the electric field strength E .
Since the pd V and the plate separation d are constant, E is also constant.
![]()
Lines of the same potential are called equipotentials . These are placed at right angles to the electric field lines. As a result of the field being uniform, the equipotential lines are equally spaced.
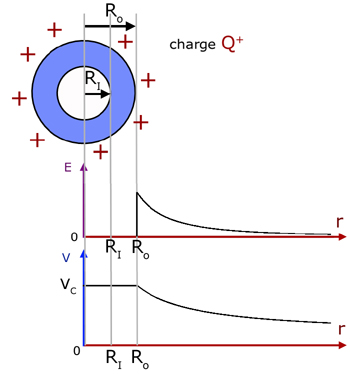
Fields in and around hollow objects
The simplest case is of a sphere.
outside of the sphere : E and V are the same as for a point charge at the sphere centre.
inside the sphere : E is zero in the material of the shell and in the enclosed space, while V is constant throughout (VC).
Deflection of ion beams
From our definition of field strength (E=F/Q) , making the force F the subject of the equation, for a small charge q related to a particle :
![]()
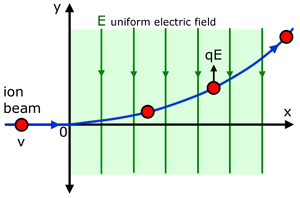
This force is constant at right angles to the original velocity v. The vertical displacement Sy of the particle can be found from one of the 'equations of motion' used in mechanics :
![]()
where,
u is the original velocity, in this case u = 0
t is the period of acceleration
a is the acceleration
Substituting for u ,
![]()
From Newton's 2nd Law of Motion,
![]()
Elimenating F , using our original expression for field strength
![]()
Rearranging to make the acceleration a the subject,
![]()
Returning to the expression for vertical displacement and substituting for a ,
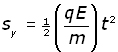
The expression for horizontal displacement SX can be rearranged to give an expression for t .
![]()
By substituting for t into the Sy equation we obtain our final expression :
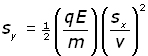
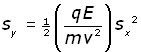
The equation is of the form y = kx2 , where k is a constant. The curve of the function is therefore a parabola.
Van de Graaf Generator
The Van de Graaf generator is a machine for producing extremely high potential differences (>107 V).
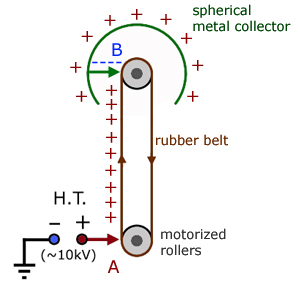
At the bottom (A), positive ionised air molecules are created at the points of a metal 'comb'. The molecules repel and are 'sprayed' onto the rubber belt.
The belt in turn takes the charges up to another comb (B). Here the charges induce negative charges which spread over the inside of the sphere. Positive charge is induced on the outside of the sphere.
At the same time, negative charges from the inside of the sphere are sprayed onto the belt to neutralise the positive ones. As the belt rotates more positive charge is taken up to the sphere and the cycle repeats itself.
Gold Leaf Electroscope
The Gold Leaf Electroscope is a simple device but effective in the following areas:
measuring electrical potential
detecting the presence of charge close to it
determining whether a charge is positive or negative
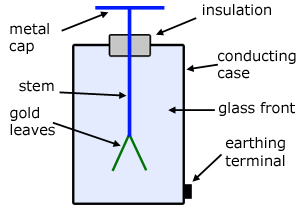
The two gold leaves are freely suspended and diverge when charged. The degree of divergence is a measure of the charge imparted.
Unfortunately space precludes a more detailed explanation of this amazing device at present.
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
