Home >> Mechanics, linear motion, uniform acceleration

Introduction

To understand this section you must remember the letters representing the variables:

u - initial speed
v - final speed
a - acceleration(+) or deceleration(-)
t - time taken for the change
s - displacement(distance moved)

It is also important to know the S.I. units ( Le   Système International   d'Unités) for these quantities:

u - metres per second (ms^-1)
v - metres per second (ms^-1)
a - metres per second per second (ms^-2)
t - seconds (s)
s - metres (m)

In some textbooks 'speed' is replaced with 'velocity'. Velocity is more appropriate when direction is important.

Displacement-Time graphs

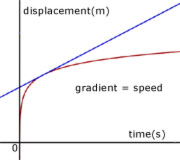
For a displacement-time graph, the gradient at a point is equal to the speed .

back to top

Speed-Time graphs

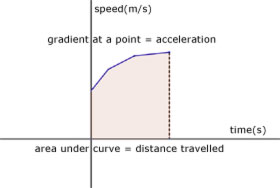
For a speed-time graph, the area under the curve is the distance travelled.

The gradient at any point on the curve equals the acceleration.

Note, the acceleration is also the second derivative of a speed-time function.

back to top

Equations of Motion

One of the equations of motion stems from the definition of acceleration:

acceleration = the rate of change of speed

rearranging,

if we define the distance 's' as the average speed times the time(t), then:

rearranging,

rearranging (i

subtracting these two equations to eliminate v,

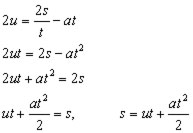
It is left to the reader to show that :

hint: try multiplying the two equations instead of subtracting

summary:

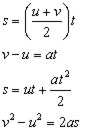
Example #1

A car starts from rest and accelerates at 10 ms^-1 for 3 secs.
What is the maximum speed it attains?

Example #2

A car travelling at 25 ms^-1 starts to decelerate at 5 ms^-2.

How long will it take for the car to come to rest?

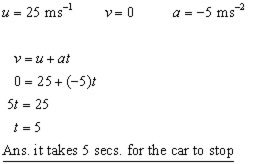
Example #3

A car travelling at 20 ms^-1 decelerates at 5 ms^-2.
How far will the car travel before stopping?

Example #4

A car travelling at 30 ms^-1 accelerates at 5 ms^-2 for 8 secs.
How far did the car travel during the period of acceleration?

back to top

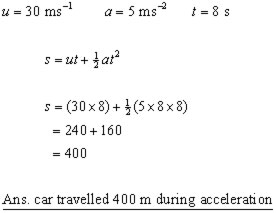
Vertical motion under gravity

These problems concern a particle projected vertically upwards and falling 'under gravity'.

In these types of problem it is assumed that:

Example #1

A stone is thrown vertically upwards at 15 ms^-1.

(i) what is the maximum height attained?
(ii) how long is the stone in the air before hitting the ground?

(Assume g = 9.8 ms^-2. Both answers to 2 d.p.)

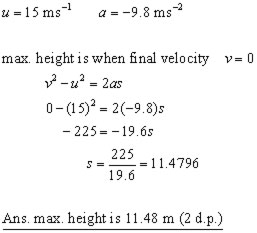
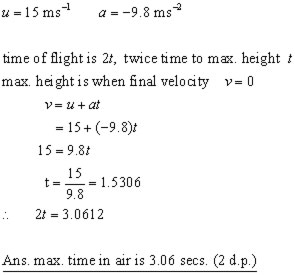
Example #2

A boy throws a stone vertically down a well at 12 ms^-1.
If he hears the stone hit the water 3 secs. later,

(i) how deep is the well?
(ii)what is the speed of the stone when it hits the water?

(Assume g = 9.8 ms^-2. Both answers to 1 d.p.)

back to top

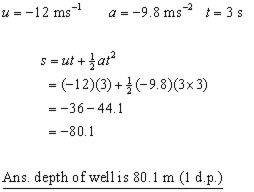
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]