Home >> Fields, magnetic fields 1
flux φ |
||
fast revision: Magnetic field lines follow the direction of a free moving North Pole.
Magnetic Flux φ (phi)
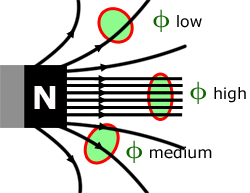
By definition, magnetic flux is a measure of the strength of a magnetic field over a given area perpendicular to it.
The diagram below shows how the magnetic flux φ over an area A varies around the pole of a magnet.
Flux Density B
We can refine the idea of flux by making the area unity (1m2). This introduces a new concept - magnetic flux density B .
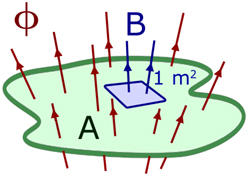
For normal area (area at right angles),
total magnetic flux = flux density x area
![]()
Units
The unit of flux is the Weber (Wb) and the unit of flux density is the Tesla (T).
A flux density of 1 Tesla is 1 Weber per square metre.
1 T = 1 Wbm-2
For an area A at an angle θ to the magnetic field, normal flux density has magnitude Bcosθ .
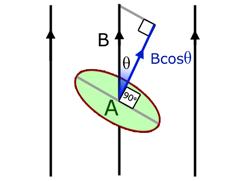
So the total normal flux over an area A at an angle θ to the field is given by :
![]()
Magnetic fields around current-carrying conductors
The magnetic field around a current-carrying wire is a series of concentric field lines. The field is not uniform. The lines are not evenly spaced. The field is non-uniform, with lines tightly packed close to the wire and widely spaced away from it.
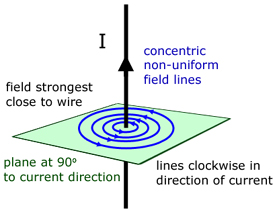
The direction of the lines of force is clockwise in the direction of the current direction.
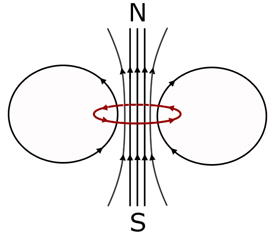
The field around a plane circular coil resembles the field around a short bar magnet.
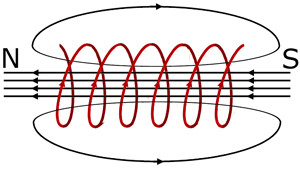
The field around a solenoid resembles the field around a long bar magnet.
Flux density for a straight wire
The diagram below illustrates the flux density B at a point P a distance a away from the wire.
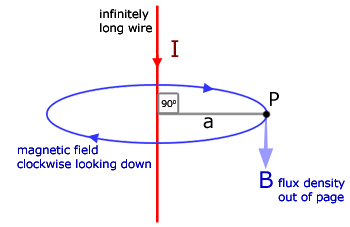
The magnetic flux density B is described by the equation :
![]()
where μo is the permeability of free space.
Unfortunatel a full derivation of this equation cannot be given at present.
Flux density for an infinitely long solenoid
The diagram illustrates the flux density B in a solenoid with n turns and coil current I.
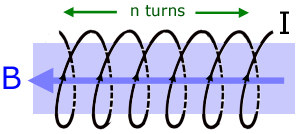
The magnetic flux density B is described by the equation :
![]()
where μo is the permeability of free space and n is the number of turns per unit length of the solenoid.
The value of B approximates to that of a real solenoid provided the solenoid's length is at least x10 its diameter.
The quantity nI is of significance. It is equal to the magnetic field strength H , with units of amp-turns/metre (Am-2) .
note: turns n has no units
![]()
Uniform magnetic fields - Helmholtz Coils
A single plane coil of radius r , turns N and current I produces magnetic flux density B at its centre.
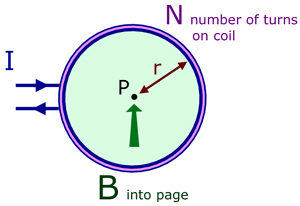
![]()
where μo is the permeability of free space.
Helmholtz Coils produce a region of uniform magnetic field within a discrete volume. Two identical plane coils are aligned along a common axis and positioned a distance r apart, where r is the coil radius.
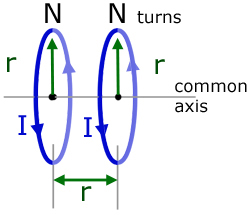
The current I passing through each coil is the same and in the same direction.
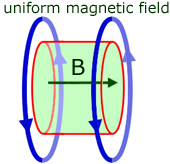
The magnetic flux density B in the volume of uniform field (shaded green) is given by :
![]()
where μo is the permeability of free space.
Helmholtz coils are particularly useful for deflecting electron/ion beams. All charged particles follow a circular path when injected into a magnetic field at right angles to their motion. By measuring the radius of a path and whether the path is clockwise or anticlockwise, important information can be gleaned on the charge of a particle and its mass.
This method is particularly important in distinguishing α , β and γ particles from each other.
[ About ] [ FAQ ] [ Links ] [ Terms & Conditions ] [ Privacy ] [ Site Map ] [ Contact ]
